A diamond net of molecular tetrahedra

What does it look like?

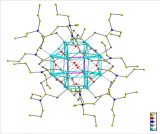
Figure 1. A ball and stick representation of a single [Cu₆(ctc)₄]₁₂- tetrahedron. Hydrogen atoms have been omitted for clarity. Colour code: Oxygen red; Carbon black; Copper blue.

For millennia philosophers and mathematicians have pondered the mysteries of the simplest platonic solid, the tetrahedron. Aristotle believed, in error, that regular tetrahedra could pack together to completely fill space, a hypothesis that endured for close to 1800 years.¹ The problem of determining their maximum packing efficiency is still being investigated today.² Perhaps a more fascinating subject for us as chemists and crystallographers, however, is the arrangement of molecular tetrahedra in crystals.

The tetrahedron described here is an anionic (Metal)₆(Ligand)₄ self-assembled coordination cage (Figure 1). The corners of the cage are formed by four tripodal cyclotricatechylene^6- (ctc) ligands. Various divalent square planar, square pyramidal and octahedral metal centres can link the organic ligands along the six edges of the tetrahedron.³

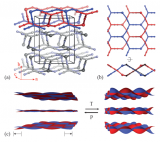
Perhaps the most interesting tetrahedron in this family is the tetrahedron generated with Cu²⁺ centres and methyltripentylammonium and Na⁺ counter cations. In this crystal lattice the tetrahedra are not permitted to adopt a dense, space filling configuration. Instead, the tetrahedra act as tetrahedral nodes to pack together in a highly symmetrical diamond-type arrangement (Figure 2). The four faces of an individual tetrahedron point directly towards the faces of four adjacent tetrahedra. The tetrahedra, which each carry a 12^- charge, are held together in this arrangement through hydrogen bonding with aquated sodium cations that are located between the faces. The cavities within the tetrahedra are occupied by crystallographically disordered methyltripentylammonium cations and solvent molecules.⁴

Figure 2. The arrangement of [Cu₆(ctc)₄]₁₂- tetrahedra of the crystal structure of (NMePent₃)₆Na₈[Cu₆(ctc)₄]₁₂.solvate. Maroon spheres represent the centroids of the tetrahedra which are arranged in adamantine (diamond) type units. Hydrogen atoms, disordered solvent and counter ions have been omitted for clarity. Colour code: O red; C black; Cu blue.

The synthesis and structural characterization of (NMePent₃)₆Na₈[Cu₆(ctc)₄]I₂.solvate were carried out in the Abrahams/Robson research labs, School of Chemistry, The University of Melbourne.

The work is published in Chemical Communications. DOI: 10.1039/c1cc12723c.

References

(1) Chen, E. R. No Title, University of Michigan, 2010.

(2) Chen, E. R.; Engel, M.; Glotzer, S. C. Discrete Comput. Geom. 2010, 44, 253.

(3) Abrahams, B. F.; FitzGerald, N. J.; Robson, R. Angew. Chem. Int. Ed. Engl. 2010, 49, 2896.

(4) Abrahams, B. F.; Boughton, B. A.; FitzGerald, N. J.; Holmes, J. L.; Robson, R. Chem. Commun. (Camb). 2011, 47, 7404.

Tags: packing   molecular