Local Order Hidden Inside the Average Order in PZN

Short Range Order, what is it and why is it tricky?

Modelling short-range order (SRO) is tricky. Since in a system with SRO you cannot assume that all unit cells are the same, conventional crystallographic ideas — like Rietveld refinement or conventional single crystal refinement of diffraction data — just don't work. These tools are useful for giving you the global average structure, but they don’t tell you about the local configurations that make up that average.

It is a bit like looking at the average of a room full of people. The average person might be 45% male and 55% female, 1.7m tall, 68kg in weight … but there is a lot more information to be had. What is the average weight of the males? Average height of the females? And, of course, the average person does not really exist, so knowing this average might not be very useful.

Similarly with materials, if we want to know how the useful properties arise from the structure and we only have the average structure, then if the system shows disorder, then this average might not ever actually occur, so doing crystal chemical calculations based on it will lead us astray.

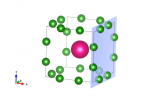
A good example of this is the family of relaxor ferroelectrics, one of the best known being PZN, PbZn_1/3Nb_2/3O₃. It is a perovskite, which we've seen plenty of this year. In this case, the PZN unit cell can be modelled by considering the Pb sites to really consist of 12 Pb sites, one along each of the [110] directions.

What does it look like?

A unit cell of PZN, with Pb (green), Zn.Nb (blue) and O (red). The Pb are modelled as 12 split sites, on each of the [110] directions.

Evidence for SRO shows up in the diffuse scattering, the scattering between the Bragg reflections. Some diffuse scattering for PZN looks like this:

Diffuse scattering from PZN, (a) in the hk0 layer and (b) in the hk1. Streaks, diamonds and other shapes are all clearly visible, all containing information about the SRO in PZN.

Now, the diffuse scattering in PZN can be modelled quite well by assuming that the Pb displace along [110] and these displacements are correlated in certain ways, and that the other atoms then relax around this Pb configuration. The problem is that these models are largely descriptive and artificial. They are based on human interpretation of the data, and do not necessarily relate directly to the underlying chemistry.

Modelling the Diffuse Scattering

In the simulation, atomic positions were swapped around and configurations kept or rejected based on whether they reduced the global instability index or not. This was after initial random distributions had been established based on the average structure. This means that the histograms of atomic separations always give the correct average and overall atomic displacement parameters, so all this SRO can be 'hidden' inside a conventional average structure.

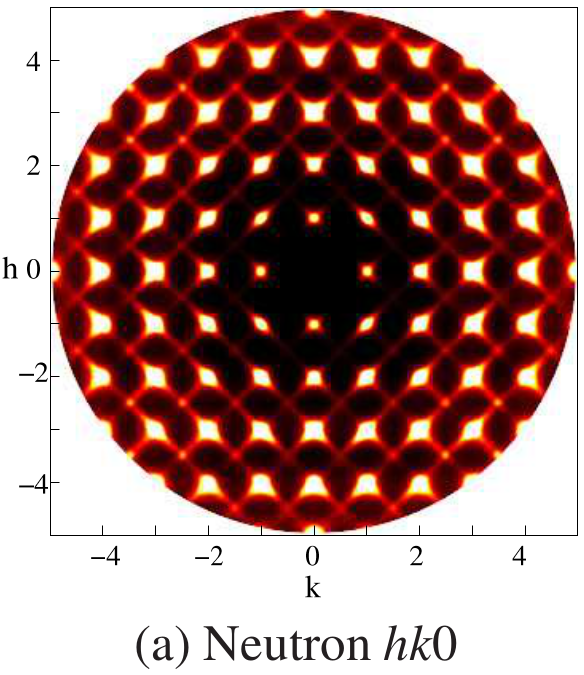
Calculated hk0 diffuse from PZN.

And this approach really can give diffuse scattering which looks a lot like the observed and which reveals what is 'inside' the average and see how the Nb behaves compared to the Zn, and so on … so below we can see that the O-Nb distances change compared with the O-Zn, even though there is no long-range order in the distribution of Nb and Zn.

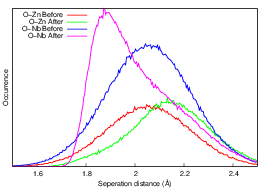
By modelling the SRO, it is possible to see how the environment around Nb is different to that around Zn, while retaining the overall average shown by conventional studies.

The highly structured diffuse scattering, and the local ordering that gives rise to it, can exist in the system without influencing the outcomes of conventional structural studies. This indicates that short-range order may be present, and crucial, and unsuspected, in many systems whose structures are thought to be thoroughly determined.

Where did this all come from?

This is all from work described in a paper by Whitfield et al.

Tags: local order   perovskite   inorganic